Definición
Una función cuadrática es aquella que puede escribirse de la forma:
f(x)= ax²+bx+c
Donde a, b y c son números reales cualesquiera y a distinto de cero.
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
Toda función cuadrática f(x) = ax2 + bx + c, representa una parábola tal que:
- Su forma depende exclusivamente del coeficiente a de x2.
- Los coeficientes b y c trasladan la parábola a izquierda, derecha, arriba o abajo.
- Si a > 0, las ramas van hacia arriba (como una carita feliz) y si a < 0, hacia abajo (como una carita triste).
- Cuanto más grande sea el valor absoluto de a, más cerrada es la parábola.
- Existe un único punto de corte con el eje OY, que es el (0,c)
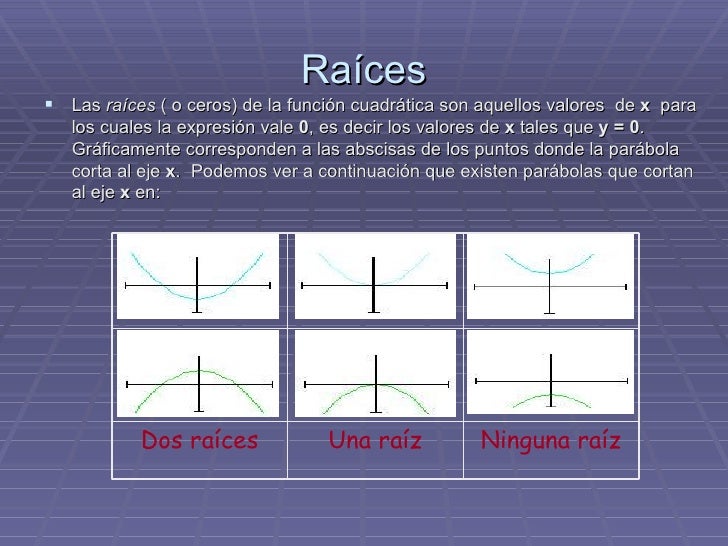
- Los cortes con el eje OX se obtienen resolviendo la ecuación ax2 + bx + c=0, pudiendo ocurrir que lo corte en dos puntos, en uno o en ninguno.
Este seria un ejemplo de si a > 0 (carita feliz)

Este seria un ejemplo de si a < 0 (carita triste)


Siempre que el término cuadrático tenga el signo positivo la parábola va a ser con las ramas hacia arriba, y si tiene el término cuadrático tiene signo negativo,la parábola va a ser con las ramas hacia abajo.
Ceros o raíces
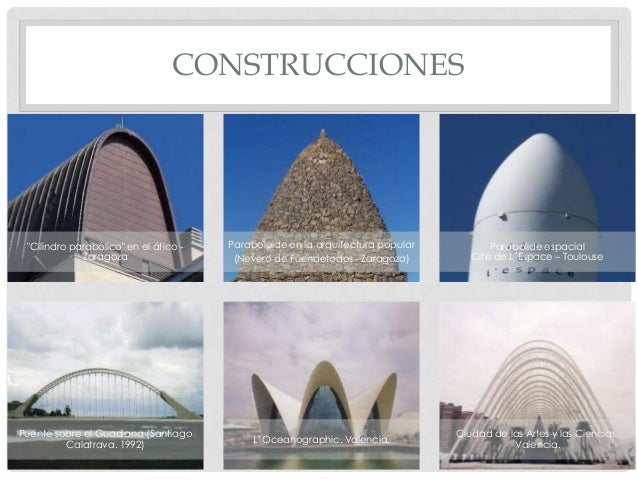
Usos de función cuadrática en la vida real
Tiene múltiples usos en la vida cotidiana aunque no nos demos cuenta.Tenemos muchas parábolas a nuestro alrededor.
Por empezar cualquier objeto lanzado al aire de forma oblicua tiene forma parabólica bajo la acción de la gravedad.
Los faros de los autos, las lámparas los micrófonos de ambiente, los satélites,antenas parabólicas en telescopios entre otros son fabricados usando propiedades de la parábola.
Otro caso es el ejemplo de los chorros de agua que salen de las fuentes, el desplazamiento bajo la acción de la atracción gravitatoria de la tierra permite obtener una bonita forma parabólica.





No hay comentarios:
Publicar un comentario